SEMANA 1
LUNES 1 DE JUNIO
Iniciamos el segundo bimestre con los siguientes temas:
Incrementos y diferenciales
Para funciones de una variable  , se define el incremento de
, se define el incremento de  como
como
y la diferencial de  como
como
En la siguiente figura se muestra  .
.

Figura 1: diferencial
Observamos que  se aproxima a cero más rápidamente que
se aproxima a cero más rápidamente que  , ya que
, ya que

y al hacer  , tenemos que
, tenemos que  .
.
Por tanto
donde  conforme
conforme  .
.
Ahora consideremos una función de dos variables
Si  y
y  son incrementados
son incrementados  y
y  , entonces el correspondiente incremento de
, entonces el correspondiente incremento de  es
es
Con lo cual  representa el cambio en el valor de
representa el cambio en el valor de  cuando
cuando  cambia a
cambia a  .
.
| Definición | |
| Sean |
Ejemplo 1
Las derivadas parciales están dadas por
de donde
JUEVES 4 DE JUNIO
MAXIMOS Y MINIMOS RELATIVOS
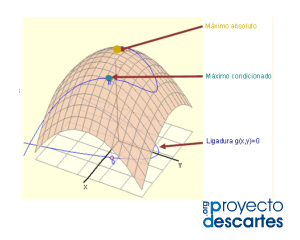
Una función f tiene un máximo relativo en el punto a, si f(a) es mayor o igual que los puntos próximos al punto a.
Una función f tiene un mínimo relativo en el punto b, si f(b) es menor o igual que los puntos próximos al punto b.
MAXIMOS Y MINIMOS CONDICIONADOS
Las restricciones o condiciones están en forma de ecuaciones o en forma de restricciones del dominio de f. Podemos resolver estos problemas por primero despejar una de las variables de las ecuaciones de restricción, para después sustituirla en f, y después ubicar el máximo (o mínimo) de la función que resulta. En casos en los que el dominio R de la función resultando tiene una frontera, tenemos también ubicar los extremos de f cuando se está restringido a la frontera.
MULTIPLICADORES DE LAGRANGE
Para localizar los candidatos a extremos relativos de una función f(x, y, . . .) sujeta a la restricción g(x, y, ...) = 0, se resuelve el siguiente sistema de ecuaciones para obtener x, y, ... y λ:
- fx = λgx
- fy = λgy
- ...
- g = 0
El incógnita λ se llama un MULTIPLICADOR DE LAGRANGE. Los puntos (x, y, . . .) que se ocurren in las soluciones son los candidatos a los extremos relativos de la función f sujeta a g = 0.
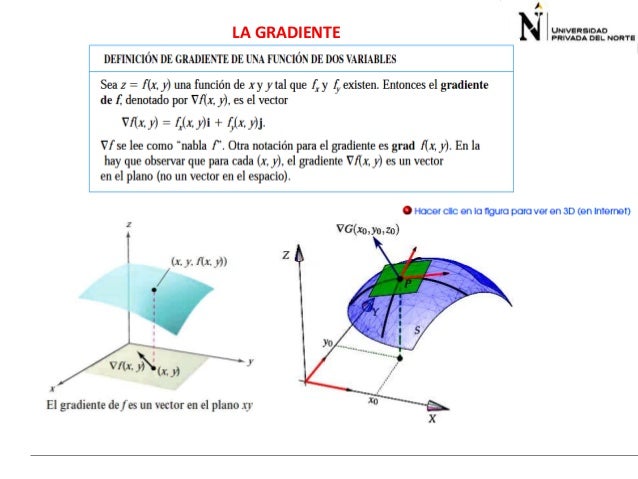
Derivada direccional y vector gradiente.
Se llaman derivadas direccional de la función z = f(x,y)
en un punto P(x,y) en el sentido del vector el siguiente límite si existe y es finito:
Para calcular este límite se toma el vector unitario de la dirección del vector (dividiéndolo por su
módulo).
Llamamos t a la longitud del vector , es decir ,con lo cual , de donde
, y el límite se reduce a la única variable t
Si la función f(x, y) es diferenciable, entonces la derivada direccional se calcula por la fórmula:
(es decir la suma de los productos de las parciales por las componentes del vector unitario)
Si la función es de tres variables z=f(x, y, z) la derivada direccional se calcula de manera análoga:
(Las parciales habrá que calcularlas en el punto correspondiente.
Las componentes del vector unitario
coinciden con los cosenos directores del vector director. Si la función no es diferenciable esta fórmula no
es válida y hay que calcular el límite anterior).
Se llama gradiente de una función z = f(x, y) en un punto P(x, y) al vector que sale del punto P y sus
componentes son las derivadas parciales de la función en dicho punto.
SEMANA 8 DE JUNIO
INTENGRALES MULTIPLES
INTEGRALES DOBLES
Al igual que las integrales de una variable sirven para calcular el área bajo una gráfica,
las integrales dobles sirven para calcular volúmenes.
Concretamente, cuando F ≥ 0, la
integral ∫ d
c
∫ b
a
F(x, y) dxdy es el volumen bajo la gráfica en el rectángulo [a, b] × [c, d], esto
es, a ≤ x ≤ b, c ≤ y ≤ d.
Lo mismo se cumple en regiones más generales. Es decir, si R es una región del plano y
F = F(x, y) es una función no negativa en ella, entonces
(1) ∫∫
R
F = Volumen bajo la gráfica de F sobre la región R

Ejemplo. Calculemos el volumen limitado por F(x, y) = 2 − x + y (esto es un plano) y
por el círculo unidad C en el plano XY . Si utilizamos la estrategia de considerar secciones
verticales en C, presentaremos el círculo unidad como
C =
{
(x, y) : −1 ≤ x ≤ 1, −
√
1 − x
2 ≤ y ≤
√
1 − x
2
}
.
De acuerdo con (1), el volumen viene dado por
∫ 1
−1
∫ √
1−x2
−
√
1−x2
(2 − x + y) dydx =
∫ 1
−1
(
(2 − x)y +
1
2
y
2
)
√
1−x2
−
√
1−x2
dx = 2 ∫ 1
−1
(2 − x)
√
1 − x
2 dx.
La última integral es un poco complicada y nos vamos a ayudar de que sabemos que
∫ 1
−1
√
1 − x
2 dx =
1
2
π
porque esta integral de una variable es el área del semicírculo de
radio 1 (área del círculo = πR2
). Entonces la integral anterior es:
4
∫ 1
−1
√
1 − x
2 dx +
∫ 1
−1
(−2x)
(
1 − x
2
)1/2
dx = 4 ·
π
2
+
(
1 − x
2
)3/2
3/2
1
−1
= 2π
SUMAS DE RIEMAN

SEMANA 24 DE JUNIO
JACOBIANO
Dada una integral doble de una función F(x, y) definida en un dominio Dxy, es posible realizar un cambio de variables para otro dominio Duv de la siguiente manera:
Sustituimos x por una función H(u, v), e y por otra función G(u, v). Entonces la integral doble resultará
J se denomina Jacobiano, y resulta de resolver un determinante formado por las derivadas parciales de las funciones H y G.
Coordenadas Polares
En ciertas ocasiones, la descripción de los dominios de integración en coordenadas rectangulares resulta más bien complicada, y se simplifica si los definimos en coordenadas polares.
Supongamos un punto genérico (x, y) dentro de un sistema de ejes cartesianos ortogonales. Si trazamos un segmento rdesde el origen de coordenadas hasta el punto (x, y), podemos determinar un vector que forma un ángulo t con el eje de las x.
Entonces tenemos a x e y como coordenadas rectangulares, y a r y t como coordenadas polares, las cuales las podemos relacionar de la siguiente manera:
x = r cos t y = r sen t.
Entonces vamos a formar el Jacobiano con las derivadas parciales de las funciones x(r, t) e y(r, t)
Como r es un radio, es siempre positivo, así que no hace falta tomarlo como valor absoluto.
Por lo tanto, la evaluación de una integral doble en coordenadas polares resultará
Coordenadas cilíndricas
Vimos que en la geometría plana presentamos el sistema de coordenadas polares con el objeto de dar una descripción más conveniente a ciertas curvas y regiones. En tres dimensiones existen dos sistemas de coordenadas que son semejantes a las coordenadas polares y proporcionan descripciones más apropiadas de algunas superficies y sólidos que suelen presentarse.
Uno es el sistema de coordenadas esféricas (que lo veremos más adelante), y el otro es el sistema de coordenadas cilíndricas, en donde un punto P del espacio tridimensional se representa mediante una tríada ordenada (r, t, z) donde r y t son las coordenadas polares de la proyección de P sobre el plano x y, y z es la distancia dirigida desde el plano x y a P como se muestra en la figura.
Entonces podemos afirmar que x = r cos t, y = r sen t, y z = z.
Supongamos ahora una integral triple de una función F(x, y, z) definida en un dominio Dx y z, podemos sustituir las variablesx, y, z por funciones H (u, v, w), M (u, v, w), y N (u, v, w) respectivamante, entonces la integral triple nos queda igual a
Coordenadas esféricas
Las coordenadas esféricas (r, j, t) se muestran en la figura, donde r es la distancia desde el origen de coordenadas hasta el punto P, j es el ángulo entre el eje positivo z y el segmento de recta OP, y t es el mismo ángulo que en las coordenadas cilíndricas.
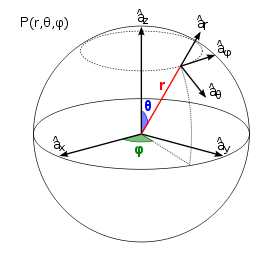
De acuerdo con estas ecuaciones vamos a calcular el Jacobiano para realizar el cambio de variables.
EJMPLO:

Aplicaciones de las integrales dobles
Las integrales dobles tienen multiples aplicaciones en fısica y en geometría. A continuación
damos una relacion de alguna de ellas:


EJEMPLO:
BIBLIOGRAFIA:
No hay comentarios:
Publicar un comentario